12. The BAMM likelihood function

12.1. Overview

This page previously discussed a number of important theoretical issues involving BAMM. We have now published a comprehensive explanation of the likelihood calculations in BAMM. See our recent Systematic Biology article and especially Sections 2.4 - 2.5 from the Supplementary Information for a detailed explanation of the BAMM likelihood function and its assumptions.

12.2. Is the BAMM likelihood computed correctly?

Given the model and its assumptions (see above), we now turn to a different question: is BAMM correctly computing the likelihood of the process described above? As an independent test of this, we implemented the BAMM likelihood function in R (BAMMtools v2.1) and have created a tool that enables users to test whether BAMM is doing what it is supposed to be doing. This assumes, of course, that we have also implemented the likelihood function correctly in R, but we hope that other researchers find it easier to evaluate our R code than the BAMM C++ code itself.

The function BAMMlikelihood will return the log-likelihood for a given configuration of events (and associated parameters) on a phylogenetic tree. Let’s do this using the built-in whales dataset in BAMMtools:

library(BAMMtools)
data(whales, mcmc.whales, events.whales)

We need to make sure we are considering precisely the same generations for the mcmc file as for the event data file, so we will get the intersection of these and just take 50 of them for some representative calculations:

iset <- intersect(mcmc.whales$generation, events.whales$generation)
iset <- iset[round(seq(1, length(iset), length.out=50))]
events <- events.whales[events.whales$generation %in% iset, ]
mcmc <-  mcmc.whales[mcmc.whales$generation %in% iset, ]

We also need to ensure that we use exactly the same segLength parameter for these calculations that were used for the BAMM analysis (see here for more info on this), as well as the same global sampling fraction (the included whales dataset was run with a sampling fraction of 0.98). Now we compute the likelihood of the final generation:

BAMMlikelihood(whales, events.whales, gen="last", segLength = 0.02, sf = 0.98)
# which returns:
        [1] -272.6831

mcmc$logLik[nrow(mcmc)]
# which returns:
        [1] -272.683

So, close – but are they close enough? Let’s do 50 samples:

rloglik <- BAMMlikelihood(whales, events, gen = "all", segLength = 0.02, sf = 0.98)
plot(mcmc$logLik ~ rloglik)
lines(x=c(-350,-250), y=c(-350, -250), lwd=1, col='red')

These should look precisely identical (please let us know if for some reason they appear to be different!). We can look at the average and maximum differences between these values:

mean(abs(rloglik - mcmc$logLik))
# which returns:
        [1] 0.0002952669
max(abs(rloglik - mcmc$logLik))
# which returns:
        [1] 0.0005066073

With this set of 50 samples, we see that the maximum difference between likelihoods computed by BAMM and by an independent R implementation is a very small number, which suggests that BAMM is doing what it should be doing. Again, this assumes that the R implementation is also correct – e.g., that we haven’t just re-implemented a set of incorrect equations into R. As one additional test, we will compute the likelihoods of a phylogeny using another implementation of the birth-death process. We will use Rich FitzJohn’s excellent diversitree package for this. The likelihoods in diversitree and BAMM aren’t exactly identical, because the diversitree log-likelihoods include a constant term sum(log(2:(N - 1))), where N is the number of tips in the tree. However, since all diversitree log-likelihoods contain this term (it is a constant that depends solely on the number of tips in the tree), we can merely subtract it to attain the BAMM likelihood (for the constant rate process):

library(diversitree)
lfx <- make.bd(whales)
constant <- sum(log(2:(Ntip(whales) - 1)))
parvec1 <- c(0.1, 0.05)
names(parvec1) <- c("lambda", "mu")

# the diversitree log-likelihood, minus the constant term
lfx(parvec1) - constant
        [1] -282.386

# BAMM log-likelihood for the same parameters:
BAMMlikelihood(whales, parvec1)
        [1] -282.386

# Another parameter set:
parvec2 <- c(0.5, 0.49)
names(parvec2) <- c("lambda", "mu")

# here's the diversitree log-likelihood, minus the constant term
lfx(parvec2) - constant # diversitree log-likelihood
        [1] -312.8122

# The BAMM log-likelihood:
BAMMlikelihood(whales, parvec2)
        [1] -312.8122

Although the diversitree functions do not (at present) allow us to compute the likelihood of a multi-process model (e.g., a BAMM event configuration with 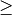\geq 1 rate shift), we can verify that BAMM, diversitree, and the BAMMlikelihood function from BAMMtools compute precisely the same log-likelihood for a given parameterization of the constant-rate birth-death process.

While we are at it, this function also allows us to estimate how much slower BAMM would be if it performed calculations in R with no calls to underlying C++ or C code. On my machine, it takes approximately 0.175 seconds to perform a single likelihood calculation (for the whales data) using the BAMMlikelihood function. For comparison, I can do approximately 10,000 generations of MCMC simulation on the same dataset per second, and the likelihood computation itself is (very conservatively) 20% of the total computation time required to execute a single generation of MCMC sampling (thus, 80% of the time BAMM is running, it is doing something other than computing the likelihood).

Using these (very rough) numbers, I estimate that BAMM can do 10,000 / 0.2 = 50,000 likelihood calculations per second. Dividing this number by the time to compute the likelihood in R, we get 50,000 / 0.175 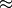\approx 280000. So, the likelihood computation using BAMM’s C++ implementation is (very) approximately 5 orders of magnitude faster than a pure R-based implementation would be for a tree of this size.

12.3. Numerical approximations in BAMM

BAMM makes several numerical approximations that we will state here explicitly.

12.3.1. Discretization of evolutionary rates for the time-varying process

BAMM uses a “fast” form of numerical integration where branches of a phylogeny are broken into segments of relative length segLength and a constant-rate birth-death process is assumed on each interval. Thus, for a time-varying diversification process, we discretize the exponential change process into units defined by segLength. This allows for much faster calculations relative to more accurate forms of numerical integration. To be clear, the likelihood itself is not approximated: it is the rates that are approximated (which may, in turn, affect the likelihood). In any event, the consequences of this are easy to test. Here, we will use the functions and data from this section and explore the consequences of segLength.

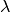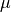If the segment size is greater than the length of a given branch, BAMM will treat the branch as a single segment (e.g., a mean value for \lambda and \mu will be computed for the branch, and they will be passed to the speciation-extinction equations for the constant-rate birth-death process). If segLength = 1.0, then no splitting will occur on any branches: mean rates will be computed for each branch. If segLength = 0.02, branches will be split into segments with length equal to 2% of the crown depth of the tree. Here are some comparisons:

# the coarsest possible discretization:
BAMMlikelihood(whales, events, gen = "last", segLength = 1, sf = 0.98)
        [1] -276.7793

# getting finer
BAMMlikelihood(whales, events, gen = "last", segLength = 0.1, sf = 0.98)
        [1] -272.7604

# the default value (BAMM v 2.5)
BAMMlikelihood(whales, events, gen = "last", segLength = 0.02, sf = 0.98)
        [1] -272.6831

# and a very fine partitioning:
BAMMlikelihood(whales, events, gen = "last", segLength = 0.0001, sf = 0.98)
        [1] -272.6776

Despite the 200-fold difference in the grain (0.02 v 0.001), the difference in log-likelihoods is marginal (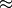\approx 0.037), and it comes at a significant computational cost (approximately 200x increase in the number of operations required to compute the likelihood). Please let us know if you find that any inferences are affected by use of the defaults for segLength.

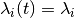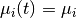For a set of time-homogeneous diversification processes, e.g., \lambda_i(t) = \lambda_i and \mu_i(t) = \mu_i, the BAMM likelihood will be exact. segLength will only influence the calculations when rates vary as a continuous function of time.

12.3.2. Maximum possible extinction probability

Some parameter values may lead to extinction probabilities that are sufficiently close to 1.0 that they are subject to numerical underflow/overflow issues. Specifically, if the 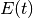E(t) equations described above take a value that is numerically indistinguishable from 1, the likelihood of the data will be 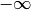-\infty. To ensure that this rejection is platform independent, BAMM automatically rejects any moves (by setting the log-likelihood equal to -INF) where the extinction probability exceeds a predetermined threshold value. This threshold is extinctionProbMax and can be set manually in the control file. Note that this is not the extinction rate: it is the maximum permitted value of 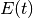E(t) in the differential equations above, or the probability that a lineage at some time (along with all of its descendants) has gone extinct before the present).